Tangent-Asymptote triangle of a Hyperbola, Part 1

While exploring a different area of math, I came across the fact that a tangential segment of a hyperbola between the asymptotes is bisected at the tangent point.

Several attempts and internet searches later, I realised that this was already known to Apollonius of Perga. Reading the Conics, it became clear Apollonius proves this through a series of propositions.

While it was a great read, I was a little disappointed at the length of the proof and wanted to find a shorter one. The content of this post consequently is the proof that I found in this regard.

Consider the hyperbola $y^2-x^2=1$. Take any point $B$ on the upper branch and draw a tangent at that point. Draw a line parallel to the tangent such that it cuts upper branch of the hyperbola at two points as shown in the following figure. We show that the midpoint of $DE$ coincides with that of $FG$.

Figure 1

The idea of the proof is to use the third dimension as well. We know that the hyperbola is the intersection curve of a cone and a perpendicular plane. 

Figure 2

If we now consider the line through $EF$ as a plane in the above figure cutting the cone, giving an ellipse as shown in the following figure. Note that this ellipse also cuts the hyperbola.

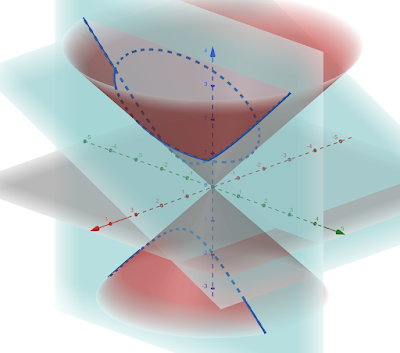Figure 3

Looking from the $x$-axis, this arrangement would look like the following figure.

Figure 4

Looking through the line perpendicular to the plane containing the ellipse, it is clear that the tangent segment caught between the asymptotes is the major of the ellipse and the segment caught between the hyperbola is a chord parallel to the major axis of the ellipse. It is clear then that the midpoints of both the segments will lie on the minor axis.

Figure 5

But looking through the line perpendicular to the plane containing the hyperbola, the minor axis is just a point proving that the midpoint of both the segments coincide.

Moving back to 2D, this property is true for all the line cutting the hyperbola. In the limiting case of a tangent line to the hyperbola, the segment caught between the hyperbola collapses to a point which is its own midpoint and therefore the midpoint of the tangential segment caught between the asymptotes.

This is very nice as we can use it give a geometric proof of $x^{-1}$ which I wasn't able to find even after an extensive internet search.

Note that Apollonius showed something more. He also proved for a given tangent, the midpoints of all the chords parallel to the tangent lie on a straight line passing through the center of the hyperbola and too for all the conics. Truly spectacular!

Until then
Yours Aye
Me

An Inversion problem from PiMuEpsilon

Often times in math, a given problem can be solved in multiple ways using algebra, geometry, calculus etc. and we try to find the shortest proof among them. But say if we are interested in Geometry, we would still look for a geometrical proof even if it is more cumbersome. This post is a perfect example of such an instance.

Let's say we a given a semicircle $C_1$ with diameter $AB$ and a circle $C_2$ with center $P$ internally tangent to $C_1$. Let the two (half) chords of $C_1$ tangent to $C_2$ and perpendicular to diameter $AB$ meet $AB$ at $R$ and $S$ respectively. Let the line perpendicular to $AB$ and passing through $P$ meet $AB$ at $Q$. We asked to prove that $PQ$ is the geometric mean of $AR$ and $SB$.

An algebraic proof is easy to find but we attempt to find a geometric one. To do that, we begin by constructing a few circles.

We first construct a circle tangent at and passing through $B$ and also is orthogonal to the blue circle, which can be constructed by drawing a tangent from $B$ to the blue circle and using the distance from $B$ and the tangent point as the radius. This is shown in orange in the next figure.

We construct another circle that is internally tangent to the green circle at $B$ and externally tangent to the blue circle. We also reflect this circle w.r.t line $PQ$. Both these are shown in violet in the following figure.

A little thought shows that the violet circle and the green circle must be inversions of each other under the orange circle.

We finally contruct another circle using the following three points (i) intersection of line $PQ$ and the orange circle and (ii) the points of intersection of the green circle and the mirrored violet circle. This is shown in red in the following figure.

We will now show that the mirrored violet circle and the green circle are inversion of each other under the red circle.

To this effect, we construct an inversion circle with center at the (lower) point of intersection of line $PQ$ and the violet circle, and make the inversion circle orthogonal to the violet circles. The inversion circle is shown in black in the following figure.

The violet circles and line $PQ$ are all invariant under this inversion.

Both the orange and the red circle pass through the center of inversion. Therefore they become straight lines. These lines can be drawn using the points of intersection of the respective circles with the inversion circle. Note that the point of intersection of the lines must lie on line $PQ$.

Line $PQ$ and the orange circle are both orthogonal to the blue circle. Therefore, their inversions will also be so. This shows the point of intersection of the orange line and line $PQ$ is the center of the blue circle's inversion. Using the fact the blue circle is tangent to both the (invariant) violet circles, we can also construct the 'inverted' blue circle.

Because the red line also passes through the point of intersection of the orange line and line $PQ$ (because the red circle passes through the intersection of the orange circle and line $PQ$), we see that the red line is orthogonal to the 'inverted' blue circle. That means, the red circle and the blue circle are actually orthogonal to each other.

As we know that the green circle and the violet circle are inversion of each other under the orange circle, we get to see that the inversion of the green circle must be the reflection of the (invariant) violet circle w.r.t the orange line.

Also, the red circle passes through the point of intersection of the green circle and the mirrored violet circle which must also be the case after inversion. Therefore we see that the 'inverted' green circle and the mirrored violet circle are reflections of each other w.r.t red line.

That clearly means that the green circle and the mirrored violet circle are actually inversions of each other under the red circle.

Because of the said inversion, we see that $FR^2=RA \cdot RA'$

But $FR=PQ$. Also, $RA'=SB$ by symmetry. Therefore, $PQ^2=AR \cdot SB$ as claimed.

Until then
Yours Aye
Me