The fact that this is impossible for $n=2$ is easy to show by inspection. Vamshi Jandhyala in our group posted grids with the required property for $3 \times 3$ and $4 \times 4$ (and eventually for $10 \times 10$) using a Python non-linear solver. However, this approach ended up time-expensive for larger grids.
He also showed such grids are impossible whenever $n=9$ or $n>10$ using a nice argument involving the number of primes between $n^2/2$ and $n^2$.
Not wanting to get into the realm of non-linearity, I log'ed the entire grid so that multiplication becomes addition and the problem becomes linear. Note that this made an Integer Non-Linear problem to a Non-Integer Linear problem. Despite precision errors, this approach worked for $n=3,4$ but proved elusive for larger $n$.
Running out of options, I eventually realised that each grid that satisfies the required property can be seen only for a particular prime (their exponents in all the $n^2$ numbers to be specific) while ignoring others.
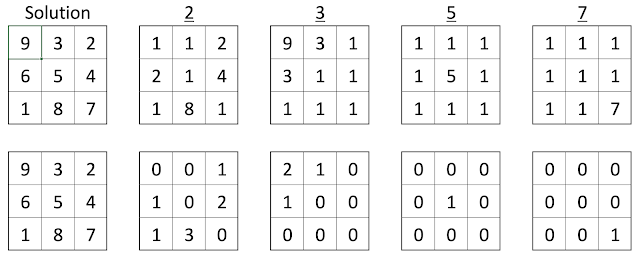
The top half of the above snapshot shows a solution to a $3 \times 3$ grid for a particular prime. The bottom half shows the same but in terms of the exponents of the prime.
The prime exponents form makes it clear that the problem can indeed be modelled as an Integer Linear Problem which can be solved extremely efficiently using free solvers in Python. In fact, doing so enables us to solve the problem for all the cases in a matter of seconds.
 |
| A Solution for $5 \times 5$ grid |
 |
| A Solution for $6 \times 6$ grid |
 |
| A Solution for $7 \times 7$ grid |
 |
| A Solution for $8 \times 8$ grid |
Python code used for solving this problem.
from ortools.linear_solver import pywraplp
import numpy as np
def main():
# Data
n = 3
vals = []
# primes = [2, 3, 5, 7, 11, 13, 17, 19, 23]
# primes = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47]
# primes = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61]
primes = [2, 3, 5, 7]
primepi = len(primes)
def vals(i0, k):
i, cnt, p = i0, 0, primes[k]
while i % p == 0:
i //= p
cnt += 1
return cnt
# Solver
# Create the mip solver with the SCIP backend.
solver = pywraplp.Solver.CreateSolver("SCIP")
x = {}
for i in range(n * n):
for j in range(n * n):
x[i, j] = solver.IntVar(0, 1, "")
for i in range(n * n):
solver.Add(solver.Sum([x[i, j] for j in range(n * n)]) == 1)
for j in range(n * n):
solver.Add(solver.Sum([x[i, j] for i in range(n * n)]) == 1)
y = {}
for i in range(n * n):
for k in range(primepi):
y[i, k] = solver.Sum([x[i, j] * vals(j + 1, k) for j in range(n * n)])
rowsum = {}
for i in range(n):
for k in range(primepi):
rowsum[i, k] = solver.Sum([y[j, k] for j in range(n * i, n * i + n)])
colsum = {}
for i in range(n):
for k in range(primepi):
colsum[i, k] = solver.Sum([y[j, k] for j in range(i, n * n, n)])
for i in range(n):
for k in range(primepi):
solver.Add(rowsum[i, k] == colsum[i, k])
solver.Minimize(1)
status = solver.Solve()
# Print solution.
if status == pywraplp.Solver.OPTIMAL or status == pywraplp.Solver.FEASIBLE:
res = []
for i in range(n * n):
for j in range(n * n):
if x[i, j].solution_value() > 0:
res += [j + 1]
print(res)
else:
print("No solution found.")
if __name__ == "__main__":
main()That eventually settles the Monkey Dog Problem of Grid multiplication. There is also an interesting question of finding $n$ which has the lowest number of solutions if rotations and reflections are identified. That could be left as an exercise to the reader.
Hope you enjoyed this. See ya later.
Until then
Yours Aye
Me